Grokking Bitcoin
How one regards Bitcoin is largely a matter of perspective. We will be looking at Bitcoin from the point-of-view of a programmer, and as a programmer we must peer into the abstractions that will allow us to meaningfully reason about Bitcoin. At the highest level of abstraction, we will regard Bitcoin as being composed of three interlocked systems (Figure 1):

Figure 1: Bitcoin’s Layered Architecture
- A Triple-Entry Accounting System to provide us with a system of Digital Cash.
- A Distributed Timestamp System to act as a public notary for our Triple-Entry Accounting System.
- An Append-Only Database to ensure that none of the nodes in our Distributed Timestamp System can modify past entries within our Triple-Entry Accounting System.This maintains an immutable, chronological record of notary entries.
A Triple-Entry Accounting System
The Triple-Entry Accounting System, as described by Ian Grigg in his 2005 paper by the same name, utilises Signed Receipts in a protocol that extends double-entry bookkeeping into a much more robust system of accounting; one that is resistant to the typical accounting fraud of maintaining multiple sets of books. It turns out that incidentally, binding participants into a multiparty payment system like that proposed for Triple-Entry-Accounting, results in a form of Digital Cash.
Let’s make digital money
Here we show how a combination of Signed Receipts managed by a Trusted Issuer can provide us with a digital cash system. Consider a simple three-party payment system, wherein Alice will be sending some amount of money to Bob via a trusted third-party, and employing Signed Receipts in the protocol.
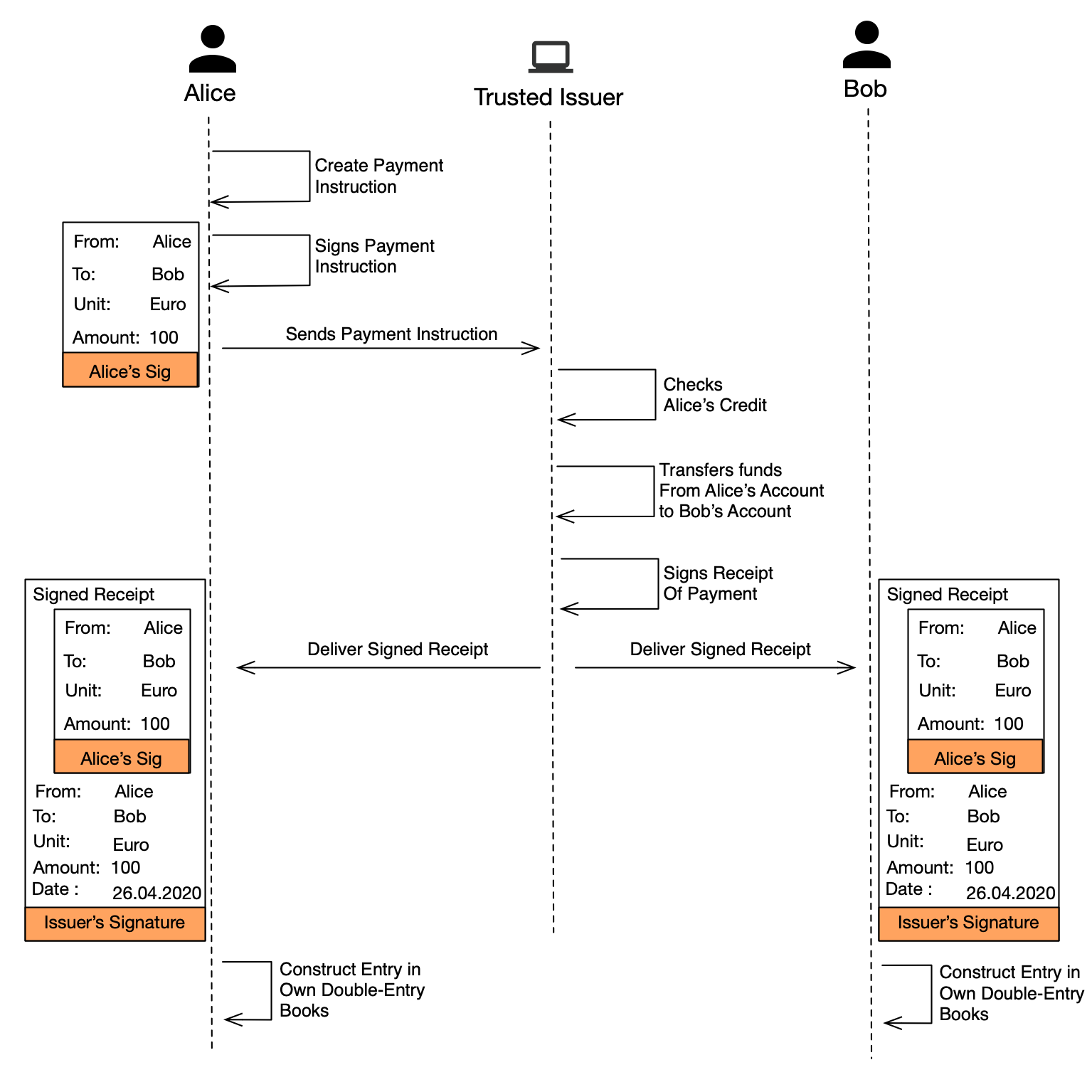
Figure 2: Three Party Payment System
Referring to Figure 2, we notice a few interesting things:
- Alice, Bob and the Trusted Issuer all have copies of the Signed Receipt. These three copies of digitally signed records is where Triple-Entry-Accounting derives it’s name from.
- Alice and Bob can reconstruct an entry for their respective double-entry bookkeeping systems purely based off the information contained in their copy of a Signed Receipt.
- For as long as the Trusted Issuer remains honest, Bob and Alice, along with any other number of other participants can use this as a system of digital cash.
Creating digital cash is that simple. If it is not immediately obvious to you where the digital cash comes from, neither Alice nor Bob can cheat the system by either spending funds they don’t have, or by claiming that they have more funds than their balance reflects. Any claims Alice or Bob might make will need to be backed up by copies of their own Signed Receipts, which can be used to expose fraudulent behaviour by either of the other two parties.
To the extent that we are interested in a robust system of digital cash, there remains the issue of trust within the honesty of the Issuer. The Issuer has the power to create money out of thin air by inventing phantom Bobs and Alices, and in so doing can “fiddle” with the money supply. In the next section we will introduce a solution to this problem by replacing the Trusted Issuer with a Distributed Timestamp System.
A Distributed Timestamp System
A timestamp system or timestamp server is a computer or network of computers that collect items in a database, and arranges those items chronologically in the order that they were received in by the timestamp system.
Let’s consider the simplest timestamp server. Figure 3.
- Records are collected into the system from lots of different sources.
- The timestamp server records the chronological ordering of the records into it’s database on a first-seen basis.
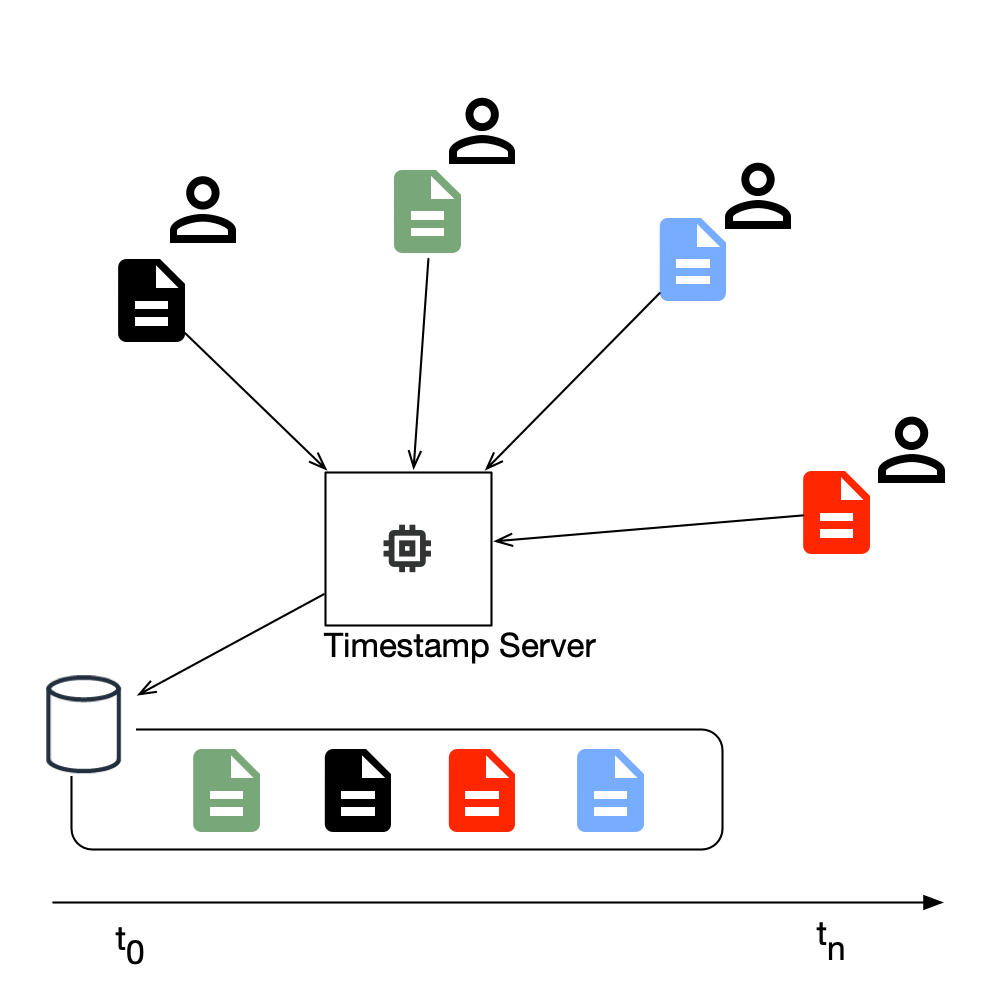
Figure 3: Timestamp Server
Now let’s consider the distributed timestamp system. Figure 4
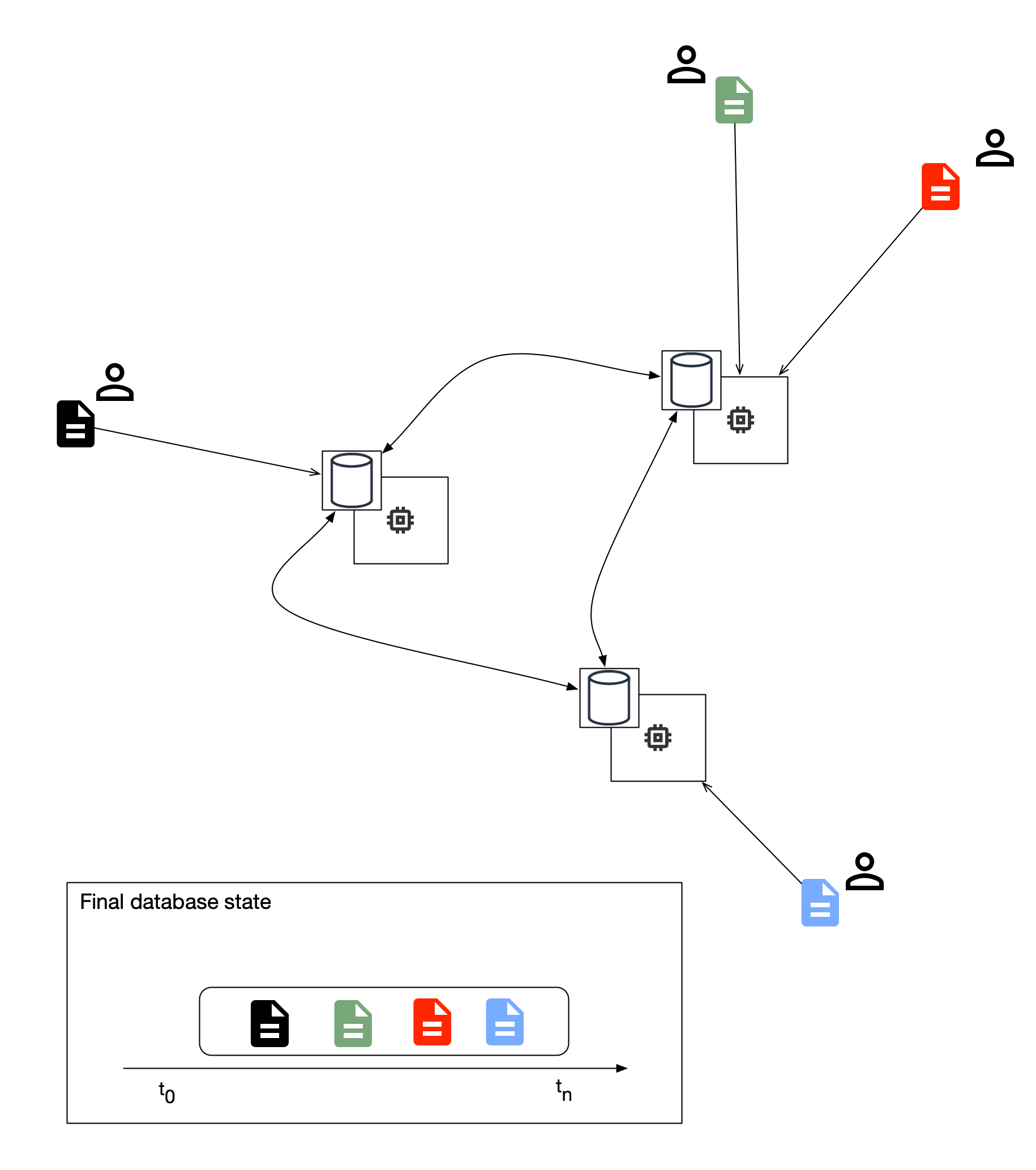
Figure 4: Distributed Timestamp System
In Figure 4 the individual nodes within our distributed timestamp system need to agree on a consistent state of their shared database. More than just settling on a consistent state, we also want to ensure that our system of digital cash can’t be corrupted by any of the participants. To the extent that our Trusted Issuer has been replaced by a distributed system of independant actors, we have come up hard against an old computer science problem known as the Byzantine General’s Problem.
Solution to the Byzantine General’s Problem
One solution to the Byzantine General’s Problem, is to engage all the individual timestamp nodes in some sort of competitive game, wherein we have a randomly distributed outcome. I.e. incentivise all the nodes to compete for a prize, with the winner being selected at random. You might have noticed that we have just created yet another problem: Who get’s to decide the winner ?
As it turns out, there is a way in which we can conduct a competition amongst a number of participants in such a manner that, on aggregate, they will win a number of rounds of the competition commensurate with the amount of effort they put forth in running the race. Put another way, winnings are aligned with how hard you tried to win. The specific way we can conduct the competition, is by requiring all participants to solve a hash puzzle, and to have the solution to that hash puzzle be calculated as a function of the previous solution. Since we require the n_th solution to use the n-1_th solution as an input, we need to have a means for the winner of a “round” to signal others that they have won. This way we keep the competition going, and everyone get’s a chance to win. Since the competitors are expending computing power to calculate the hash puzzle, it follows that the more computing power you have, on average, the more rounds of the competition you will win.
An Append-Only Database
We will use our solution to the Byzantine General’s Problem as a signalling device amongst the nodes in our distributed timestamp system. There exists an interesting paper from 2002, which describes how one might collect all the timestamp entries in a timestamp node into a binary tree of hashes. We will require our nodes to bind the root of this binary tree into the hashpuzzle that they are calculating. This way we will have a means of synchronizing our distributed database and prevent a nefarious alteration of the timestamped records.
An early paper on how a timestamp system can construct the internal state of a set of timestamped entries is Design Of A Secure Timestamping Service With Minimal Trust Requirement, July 2002, by H. Massias and X. Serret Avila.
This paper describes assembling the hashes of the entries/documents into a binary tree data structure, with the root of the binary tree being itself a hash value calculated by the nodes immediately under it.
In using the method of constructing a linked-list of timestamped entries, consecutive entries will be calculated as follows…
Round (n) of the competition:
Block_n = HashPuzzle( Block_n-1, timeStampedEntries_n )
Round (n+1) of the competition:
Block_n+1 = HashPuzzle( Block_n , timeStampedEntries_n+1 )
Our distributed database now consists of a sequence of blocks bound into a timechain, and each block is constructed by combining the timestamped entries/documents into a binary tree using our secure timestamp method. The nodes in our distributed timestamp system will reject blocks which can’t be validated for internal consistency w.r.t the records of Signed Receipts.
Our system of digital cash now has a highly robust Issuer, and it has become that much harder for any participant or group of participants in the system to cheat the others.
Economic Incentives
Our investigation into our Distributed Timestamp System’s architecture in the previous sections neglected to account for why a node (and by extension the node operator) would perform the computationally expensive proof-of-work function in the first place.
Within our Signed Receipt, we did not require either Bob or Alice to pay any fees to the Issuer for the service of keeping an accurate account of their monies. We shall do so now. When Alice sends money to Bob, she will be required to create, as part of her payment instruction to Bob an additional entry that authorizes a small fee to be paid to the Issuer.
A mechanism for bootstrapping our digital cash system would be to allow the Issuers in our distributed timestamp system to issue a set amount of digital cash to themselves at each winning round of “hashpuzzling”. Initially though, as the digital cash economy would be non-existent, this bootstrapped expenditure of computational power would be altruistic, with the hope that the digital cash tokens might acquire a value in future that would allow the initial set of bootstrapping node operators to recoup their investment.
Our explorations into how the above concepts apply to Bitcoin is still incomplete. Once we have worked through a thorough look at Bitcoin Script, We will revisit this topic in the section on Transactions, and complete our understanding of Bitcoin as a Triple-Entry Accounting System.